
はじめまして。GaudiyでMLエンジニアをしているMomijiと申します。主に推薦システムの開発を担当しています。
今年4月から、Gaudiyが開発・提供するプロダクト「Gaudiy Fanlink」に協調フィルタリングベースの推薦機能を追加したので、本記事ではそのロジックとシステムアーキテクチャについて書いてみたいと思います。
1. 「Gaudiy Fanlink」における推薦
Gaudiy Fanlinkは、IPファンが集う、SNS型のコミュニティプラットフォームです。そこにおける「推薦」の役割は、ユーザーとコンテンツのマッチングを促進し、コミュニティ内の活動総量を増加させることにあります。マッチングを促進するためには、まずユーザーの嗜好にあったコンテンツを提示し、より多くのコンテンツにアクセスしてもらうことが重要です。
推薦システムを導入する以前は、閲覧者が "能動的に" 自分の好きな投稿作品を探す必要があり、ユーザーとコンテンツのマッチングが効率的にデリバリーできてない状況でした。実際に、熱量の高いコアな制作者が集うIPコミュニティにおいても、「制作物を投稿 → 多くの人に閲覧される → リアクションで盛り上がる」というサイクルをいかに築けるか、が目下の課題でした。
これに対して、閲覧者が "受動的に" 好みの投稿に出会うことができれば、投稿の閲覧数やリアクション数の底上げにつながると考え、推薦システムを導入することにしました。
推薦には、そのロジックをCollaborative FilteringとContent Based Filteringとで大別する考え方があります。Collaborative Filteringでは、嗜好に関するユーザ行動をスコアリングし、推薦を設計します。一方のContent Based Filteringでは、コンテンツの表現を生成し、ドメイン情報を組み込んだ推薦を設計します。
Gaudiy Fanlinkは単一の汎用プラットフォームではなく、複数のIPに特化したプラットフォームです。そのため、高度なドメイン情報のインプットを必要とするContent Based Filteringでは、IP毎の最適化において考慮すべき項目が多く、推薦システムの導入スピードが遅くなってしまう懸念がありました。
一方、Collaborative Filteringでは、アイテムへの嗜好とみなすユーザ行動を各コミュニティで考えて設計することができます。そこで初手としては、Collaborative Filteringによる推薦システムを構築することにしました。
2. 協調フィルタリングによるパーソナライズ推薦
Collaborative Filteringのアルゴリズムとして、今回はiALS(Implicit Alternating Least Squares)を採用しました。iALSは行列分解(Matrix Factorization)のアルゴリズムの一種です。
前提は省きますが、Funk-SVD ⇨ ALS ⇨ iALSという流れがあり、ユーザー数とアイテム数が多い状況でも並列計算による高速化ができる点、そしてユーザーがアイテムに対して嗜好を明示しない(Implicit Feedbackしかない)状況に対応している点が、重要な特徴です。
2-1. 学習
ユーザーのアイテムに対する嗜好をスコアリングして評価値とする。アイテムに対するクリック、いいね、リプライなどから評価値を決定します。
次にこの評価値をユーザーxアイテムとなる評価値行列として定義し、これをユーザーの行列Wとアイテムの行列Hに分解することを考えます。行列分解は損失関数を最小化するようなWとHを求めることで行われます。iALSにもいくつかの損失関数の定義がありますが、ここでは下記の定義をしています。
第一項は、分解したWとHが元の評価値行列を近似できているかどうかを評価しており、観測されているユーザーとアイテムのペア要素について、WとHから再現した評価値行列の差を最小化しています。第二項は、評価値が得られていない要素が大きな値を取らないように、ペナルティを課しています。第三項は、汎化のための正則化項です。
この損失関数をWとHについて交互に最適化します。分離可能であるため、各ステップのWとHは各ユーザー,アイテムについて並列で更新することができます。例えばユーザーの行列Wでユーザーuのベクトルについて最適化する場合、Hを固定した状態で
による偏微分が0となるときの
を求めることになります。
アイテムについても同様に以下のように記述できます。
なお第二項の部分は、実は全ユーザーまたは全アイテムに対して共通となります。よって並列計算の前に一回だけ計算しておけばよい値となり、元論文では”Gramian trick”と呼ばれている、計算量の削減が可能な部分です。
2-2. バッチ推論
学習バッチで得られた行列WとHから、をそのまま計算してユーザーごとに推薦候補を得ることができます。最後にソートロジックなどを適用してキャッシュしサービングします。
2-3. リアルタイム推論
ユーザーの評価値が更新されたら、ユーザベクトルをリアルタイムで更新することができます。なお更新と書きましたが新規のユーザーに対しても、評価値があれば推論可能です。
基本的には学習バッチと定式は変わらないので詳細は割愛しますが、計算負荷はそこそこ高いので、スループットやレイテンシに課題を感じたら、適宜高速化したり、近似したりして計算します。
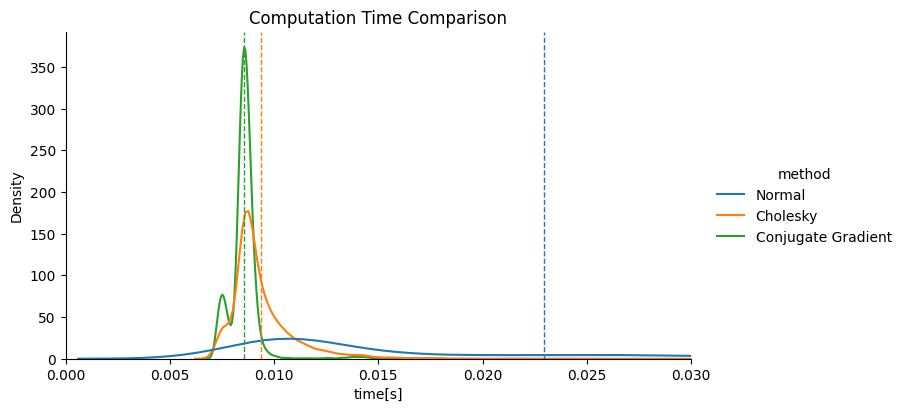
有名どころとしてはコレスキー分解や共役勾配法などがあります。簡単なシミュレーションを示しますが、通常の逆行列計算と比較してコレスキー分解はより早く、共役勾配法は適切なイテレーションで打ち切ることでロングテールを改善しているようです。ただし打ち切るイテレーションについては、推論精度を確認して決定することが望ましいです。双方ともScipyの実装があります。
3. システムアーキテクチャ
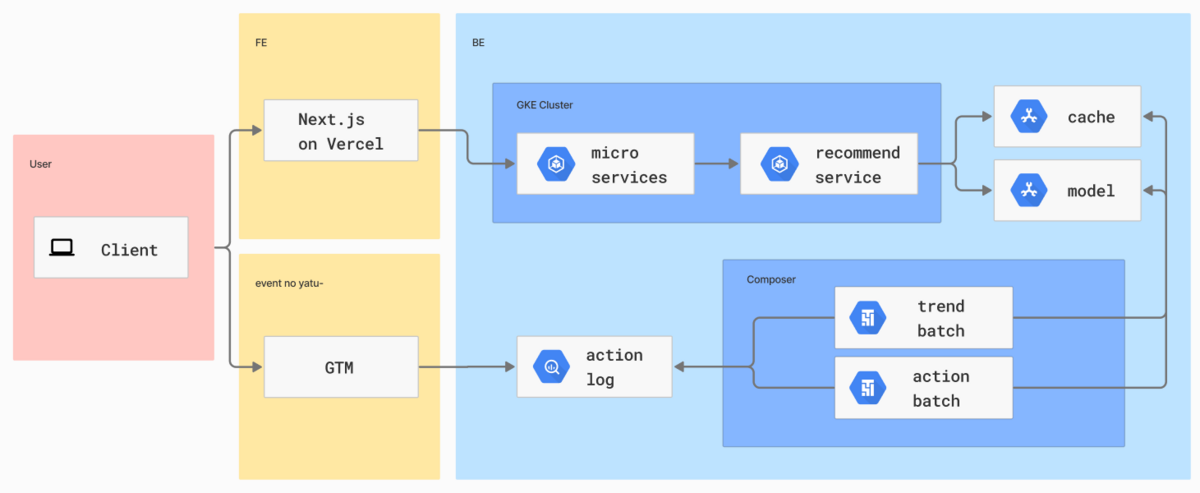
今回の推薦システムの構築は、GaudiyがCloud RunからGKEへ移行していたタイミングで実施しました。GKE移行についてはこちらの記事を参照いただければと思います。
推薦システムも流れに合わせ、バッチとサービスを両方GKEで構築しています。なおバッチはCloud Composerで構築しているので、かなり簡単に構築できました。(SREチームには大変お世話になりました。)
細かい点ですが、リアルタイム推論は近似解を利用したとしても一定の計算リソースを消費しますし、アイテム行列やGramian trickの行列を保持しておく必要があるため、メモリも十分に確保しておく必要があります。そこでML用に専用のノードプールを用意し、ユーザー、アイテムスパイクで他のマイクロサービスのリソースを圧迫しないようにしています。
4. これから
今回のリリースは複数の機能が同時リリースであったこともあり、推薦機能の導入による具体的な効果までは分析できていません。現在ABテストを実装しているので、結果については追って報告できればと思います。
また推薦候補でのパーソナライズは、ユーザー数が増加するといずれ難しくなると考えています。よってクラスタリングやグラフベースの候補生成も視野に入れています。
さらに今回のリリースではビジネスユースケースでのソートのみが実装されていますが、推薦候補に対するRerankingも重要であると考えています。こちらはユーザー行動と事業KPIとの紐付きをモデリングするところから始めています。(推論の大部分をバッチに寄せつつも、サービスレイヤが存在する上のアーキテクチャも、Rerankingを考慮しての構成です。)
最後に、Gaudiy Fanlinkはファンコミュニティであるという性質上、ドメインが多種多様で、その一つひとつがとてもディープです。私たちはこれに対して、マルチモーダルデータの活用により対応しようとしています。
現在Embeddingモデルの基礎研究やマルチモーダルLLMに関する研究開発を絶賛推進中です。こうした取り組みに興味のある方がいれば、ぜひお話しさせてください。Gaudiyでは一緒に取り組んでいく仲間も募集しています。