Gaudiy Tech Blog

Gaudiyの技術、開発組織、カルチャーについてお伝えするブログです

ECDSA署名の数学的理解とCloud KMSによる実装

こんにちは！ファンと共に時代を進める、Web3スタートアップのGaudiyでエンジニアをしている椿（@mikr29028944）です。

先日、Gaudiyではサーバーサイドウォレットの構築やEthereumにおけるECDSA署名の実装を行いました。

そこで今回は、少しニッチではありますが「ECDSA署名」をテーマに、Gaudiyの事業背景から、ECDSAの数学的な処理とコードまでを、実例をふまえてお伝えしてみたいと思います。

はじめに断っておくと、僕は大学時代にzk-SNARKsの理論を研究していたため、代数学を学んだことはありますが、この領域における専門家ではありません。なので理解が誤っている部分があれば、ぜひご指摘いただけると嬉しいです。

Web3スタートアップで働くことに興味がある方や、ブロックチェーンを業務で扱うエンジニアの方にご参考になればと思い、詳しく書いていたら1万5千字を超えてしまいました…。

以下の目次から、興味あるパートだけでもよければご覧ください！

1. GaudiyがECDSA署名を扱う理由

Gaudiyでは、ブロックチェーンを活用したファンコミュニティサービスを開発・提供しています。

そのコミュニティでは、ユーザー体験を考慮して、これまではガス代のかからないプライベートチェーン上でNFTを発行していました。それを今回、ユーザー同士でアイテムのトレード（二次流通）を行ったり、NFTとしての価値を感じられる体験を提供するために、EthereumやPolygonといったパブリックチェーン上へと書き出す（ブリッジする）機能を実装することになりました。

しかし、すべてのデジタルアイテムを、ユーザーが好き勝手に書き出せてしまうのには問題があります。

なぜなら、Gaudiyではマンガ、アニメ、ゲームなどのIP（知的財産コンテンツ）公式コミュニティをつくっており、そのコミュニティ内で配布されるアイテムもIPに紐づく画像などが多いため、著作権にも関わります。なので、あくまで「許可されているアイテムのみ書き出せる状態にしたい」というのが要件としてありました。

この課題を解決するため、サーバーサイドウォレットを作成して、Gaudiyからユーザーに対して「あるアイテムに対して書き出し可能な証明書」を発行することで、管理者の署名がないとアイテムを引き出せないようにする仕組みをつくることになりました。

ここで使われている「ECDSA」による署名や検証の方法について、Gaudiyでの実例も交えてお伝えしていきます。

2. ECDSA署名とは何か

ECDSA（Elliptic Curve Digital Signature Algorithm）とは、楕円曲線DSAとも呼ばれており、ビットコインやイーサリアムの文脈では特にトランザクションの署名に使われます。

▼こちらの記事がわかりやすいです。

zoom-blc.com

ECDSAを理解するには、前提知識として「楕円曲線暗号」を知る必要があるので、まずはその概要から説明していきます。（実例だけ知りたい方は、4. まで読み飛ばしていただいても大丈夫です。）

2-1. 前提知識としての楕円曲線暗号

2-1-1. ざっくりとした楕円離散対数問題

そもそも楕円曲線暗号とは、楕円曲線上で組み立てられた暗号プロトコル全般を指します。

近年、RSAに変わる公開鍵暗号として注目されており、RSAよりも短い鍵長で同じくらいの安全性を持つという特徴があります。実際に身近で使われている例としては、デジタル放送における映像コンテンツの著作権保護技術や、ICカード、SSL/TLSなどがあります。

後ほどより具体的な楕円曲線の話をしますが、この章では簡単に楕円曲線暗号の概念を解説したいと思います。

ある地図の上でゲームのキャラクターが歩き回ることを考えてみてください。

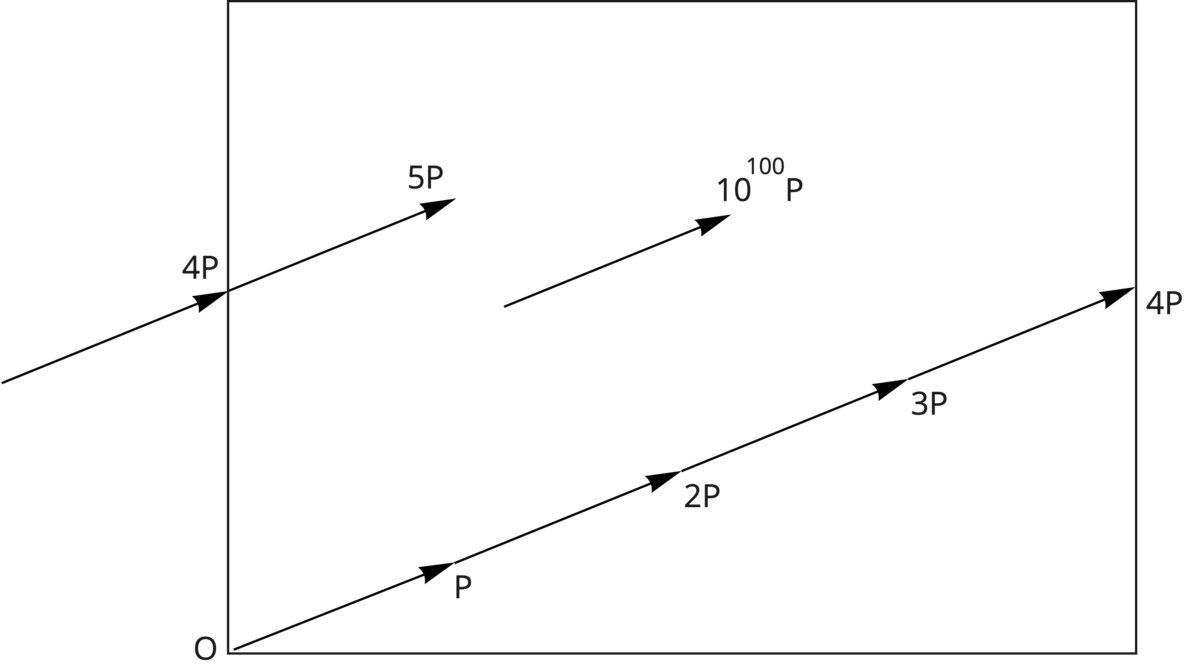
このゲームの世界では、地図から歩いて右方向に突き抜けても、反対側から同じ角度で出てくることにします。ゲームキャラクターが歩幅{P}で原点{O}から一定な角度をつけて歩くとします。２歩進むと{2P}の位置にいます。これを10回、100回…と続けても{10P,100P, 10^{100}P}と容易に位置を求めることができます。

しかしこの世界では、キャラクターが何歩歩いたかを忘れてしまった場合、今いる位置と自分の一歩から何歩歩いたかを求めようとすると、とても難しいことが知られています。一歩{P}が決まっている時に

歩数nから現在地nPを求めることは容易だが、現在地nPからnを求めることは難しい

という関係性が成り立ちます。一般に「有限体 \Bbb{F} _ {p}上の楕円曲線上の点 nPと Pが与えらた時に nを求めよ」という問題を楕円曲線離散対数問題と言います。（地図を楕円曲線として変換しています）

また、この問題を利用して、楕円曲線暗号では nPを公開鍵、 nを秘密鍵として、「公開鍵から秘密鍵を現実的な時間で求めることが難しい」ことを安全性要件としています。

（以下の参考書から例を抜粋しています）

クラウドを支えるこれからの暗号技術 | 光成 滋生 |本 | 通販

2-1-2. 楕円曲線暗号

では実際に、代数的な側面から楕円曲線上の加算と楕円曲線離散対数問題について考えます。

pを大きな素数として、有限体 \Bbb{F} _ p上の楕円曲線は、以下のような3次方程式で定義されます。

4a^ 3+27b^ 2 \not = 0かつa, b \in \Bbb{F} _ pとする。以下では下式の楕円曲線を Eと表します。

\tag{*} y^2= x^3 +ax +b　

楕円曲線上の有理点の集合の全体は以下のように定義する加法について群をなすことが知られています。

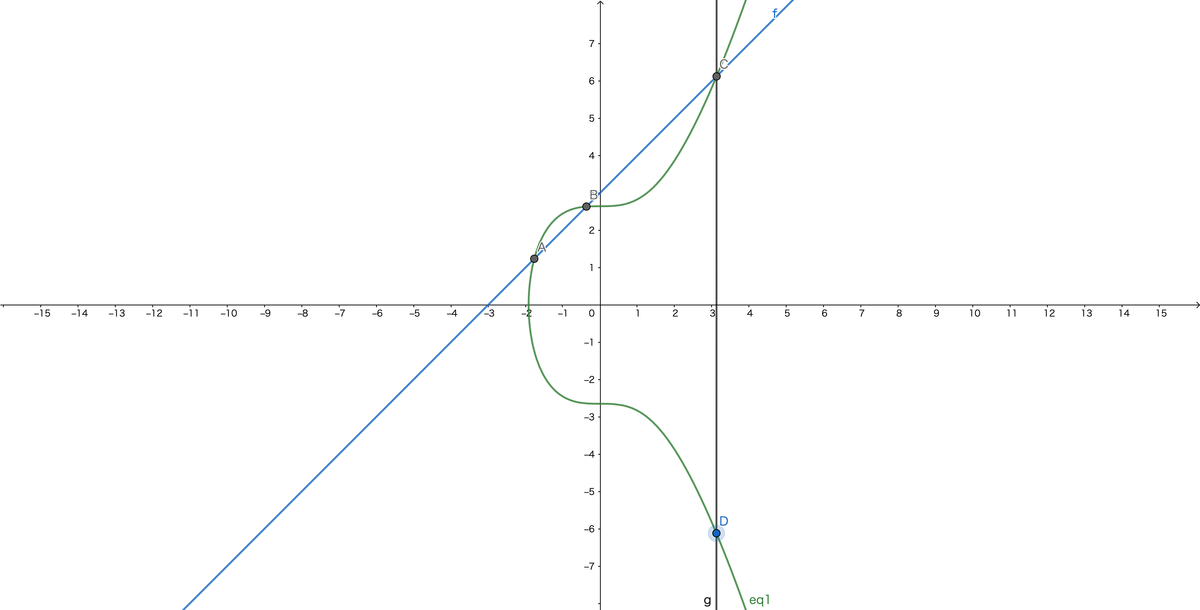
曲線上の点 Aと点 Bを足した点 Dは、点 A、 Bを結ぶ直線が再び曲線と交わる点 Cの y座標の符号を反転した点で定義されます。点 A、 Bが同じ点である場合は、その点で接戦を引きます。また楕円曲線上の点として、無限遠点 Oと呼ばれる仮想的な点を定義します。さらに無限遠点 Oとある点 Pの加算結果は、点 Pになると定義します。

この時、曲線上の点 Gがある場合に、上記の方法でその点を k回加算する演算（スカラー倍算呼ぶ）と、自然数 kから点 W=k \times Gを満たす自然数 kを求める演算は、容易に求めることができます。一方で、このスカラー倍算の逆演算（２点 Gと Wから、 W = k \times Gを満たす自然数 kを求める問題）は楕円曲線離散対数問題と呼ばれ、自然数 kの桁数が大きくなるほど解くのが難しいと言われています。

まとめると、楕円曲線暗号は、この「楕円曲線上の離散対数問題」を用いて構成される暗号のことを言います。

次に、この楕円曲線上の離散対数問題を利用したECDSAによる署名と検証について考えていきます。

2-2. ECDSAによる署名と検証

アリスが自分の公開鍵を使って、ECDSAによる署名と検証を行うことを考えます。

  1. 公開設定：有限体 \Bbb{F} _ p上の楕円曲線 Eと点 P（素位数 lの巡回群の生成元）を選びます。また、ハッシュ関数 hを選びます。

  2. 鍵生成：まずアリスはランダムに a \in \Bbb{F}^{*} _ {l}を選び、 A = aPとします。このとき aをアリスの秘密鍵、 Aをアリスの公開鍵とします。

  3. 署名：ランダムに k \in \Bbb{F} _ {l}^{*}を選び、 kPの x座標を rとします。平文 mに対して、以下のように s求めて (r, s)を mに対する署名とします。以下では下式を s \equiv k^{-1}(h(m) + ar) \bmod lと書きます。

    \tag{1} 　s \equiv {(h(m) + ar) \over k} \bmod l

  4. 検証： u \equiv s^{-1}h(m) \bmod l、 v \equiv s^{-1}r \bmod lを計算し、 x座標に関して、 \bmod lで以下の式が成り立つことを検証します。

\tag{＊}　uP +vA = k P

A= aPより

uP + vaP = kP

楕円曲線のスカラー倍算より

(u + va)P = kP

u, vより

(s^{-1}h(m) +s^{-1}ra)P = s^{-1}(h(m)+ra)P = kP

左辺に (1)を代入して、

(k^{-1})^{-1}(h(m)+ar)^{-1}(h(m) +a r) = kP

となり、右辺の kPと一致することがわかり、正当な署名であることの検証ができました。では次に、ここで定義した変数や処理を用いて話を展開していきます。

3. EthereumにおけるECDSA署名

3-1. secp256k1と呼ばれる楕円曲線

先ほどECDSA署名の処理を構築した際に a, bなどの多数の変数を用いました。これらは、なんでもかんでも自由に決めていいわけではありません。脆弱性のあるパラメータで楕円曲線暗号を構築した場合、計算量が多項式時間で解けてしまう攻撃手法SSSA法、準指数関数時間で解けてしまうGHS法などのあらゆる攻撃手法によって、簡単に楕円曲線離散対数問題が解けてしまいます。こういった攻撃手法の適応条件に合わないようにパラメータを選定する必要があります。

NIST（⽶国⽴標準技術研究所）やSECG（The Standards for Efficient Cryptography Group）と呼ばれる楕円曲線暗号の商用的な標準仕様を査定している機関が、安全な楕円曲線暗号を作るための推奨パラメータを公表しています。詳しくはSEC 2: Recommended Elliptic Curve Domain Parametersをご覧ください。

Ethereumでは、SECGが推奨パラメータとして公表している中の一つである「secp256k1」を使用しています。この楕円曲線から、公開鍵や秘密鍵の生成がされています。パラメータ T = (p, a, b, G, n, h)はそれぞれ以下の値になり、 (*)で定義した楕円曲線に a, bを代入すると以下のような方程式になります。

y^2 = x^3 +7

後の章で nを用いた話があるのでここで説明しておくと、パラメーターに含まれる nとは、楕円曲線上の点 Gが与えられた時に n \times G = Oとなる正の整数であり、この nを Gの位数と呼びます。群の位数、元の位数の定義などはこちらの記事がわかりやすいです。

secp256k1でのパラメータ T = (p, a, b, G, n, h)は以下のような値になっています。

Recommended Parameters secp256k1

詳しくはこちらのRecommended Parameters secp256k1セクションをご覧ください。

3-2. EthereumでECDSA署名を扱う

では実際に、secp256k1の楕円曲線上のECDSA署名がどのように行われているのかをみていきます。

詳しいEthereumにおけるECDSA署名の仕様はこちらのEthereum Yellow Paperをご覧ください。

\text{signature} = (r, s, v)

EthereumにおけるトランザクションはECDSAによる署名がされ、32バイトの r値と s値、1バイトの v値を連結した65バイトを署名とします。 r値と s値に関しては先ほど記述した値になり、 v値に関しては x座標が rとなる点 Rを一意に定めるための値になります。

もし vが 0の場合は Rの y座標の値が偶数、 vが 1の場合は Rの y座標の値が奇数を表します。 v値に関しての詳細は、後述するEIP-155と一緒に説明します。またECDSA署名が有効な場合は、以下の条件が成り立ちます。

\begin{aligned} 0 < &r < \text{secp256k1n} \\ 0 < &s < \text{secp256k1n}/2 +1 \\ &v \in \lbrace 0, 1\rbrace \end{aligned}

\text{secp256k1n}とは、前述した n \times G = Oとなる基点 Gの位数 nのことです。 rの取りうる範囲が 0から \text{secp256k1n}まで、 sの取りうる範囲が 0から \text{secp256k1n/2 +1}まで、 vは 0か 1の値を取ります。

rが \text{secp256k1n}までである理由はわかると思います。なぜなら、 \text{secp256k1n}は先ほどのECDSA署名の Gの位数 lにあたり、計算が \bmod l上でされているため、 rが lを超えないことがわかります。ですが、 sは \text{secp256k1n}までではなく、 \text{secp256k1n /2} +1までになっています。この理由は後述する「 sの反転」の章でEIP-2の概要説明と一緒に説明します。

また、署名から公開鍵の復元に関しては、平文 mのハッシュ値と r, s, vからリカバリできることがわかります。これに関しても後述します。

ここで記号を整理します。

  • G：ベースポイント、基点と呼ばれる楕円曲線上の点（ECDSAによる署名と検証章の Pにあたる）
  • h(m)：平文 mのハッシュ値（ECDSAによる署名と検証章と同じ）
  • k：署名ごとに異なるランダムで一時的な秘密鍵（ECDSAによる署名と検証章と同じ）
  • n： Gの位数 （ECDSAによる署名と検証章の lにあたる）
  • r, s： mに対する署名（ECDSAによる署名と検証章と同じ）

4. GaudiyではどのようにECDSA署名を行っているのか

ここからは、Gaudiyのユースケースを元にしたECDSA署名と検証フローを、実際のコードを添えて説明します。

4-1. 署名と検証の流れ

  1. digestと呼ばれるあるメッセージのSHA256ハッシュ化された値と、KMSに保存されているGaudiyの秘密鍵からKMSによる署名が生成されます
  2. この署名はASN.1と呼ばれる標準的なデータ構造から成るため、Unmarshalによって r, sをリカバリします
  3. rに対する v値を計算し、 (r, s, v)を連結してそれをECDSAによる署名とします
  4. Ethereumのコントラクト上でこの署名が検証され、それによってリカバリされた公開鍵と署名を作成した公開鍵が一致するかを検証します

4-2. 詳細と実際のコード

4-2-1. Cloud KMSを使ったECDSA署名の構築

Gaudiyでは、秘密鍵の管理として、Cloud KMSを活用しています。

下記の記事にもあるのですが、プライベートキーを環境変数経由で渡す場合の問題点として

  • 秘密鍵を直接使えばプログラム以外の意図しない文脈で署名を行える
  • 秘密鍵を誰が使用したという履歴はどこにも残らない
  • 秘密鍵を直接持ち出せば退職者であっても署名を行える

が挙げられます。

zenn.dev

記事ではAWS KMS（Key Management System）を使ってこれらの問題を解決していますが、Gaudiyでは同じくEthereumの署名アルゴリズム、secp256k1をサポートしている Cloud KMS を使って解決することになりました。

Cloud KMSでは、非対称署名アルゴリズム、非対称暗号化アルゴリズムなどの様々なユースケースに対応できるように鍵のアルゴリズムを設定できます。

今回のケースでは楕円曲線署名を行いたいので、非対称署名アルゴリズムを選択し、曲線の種類をsecp256k1とします。Cloud KMS関する詳細はこちらをご覧ください。

Cloud KMSの鍵の扱いについて

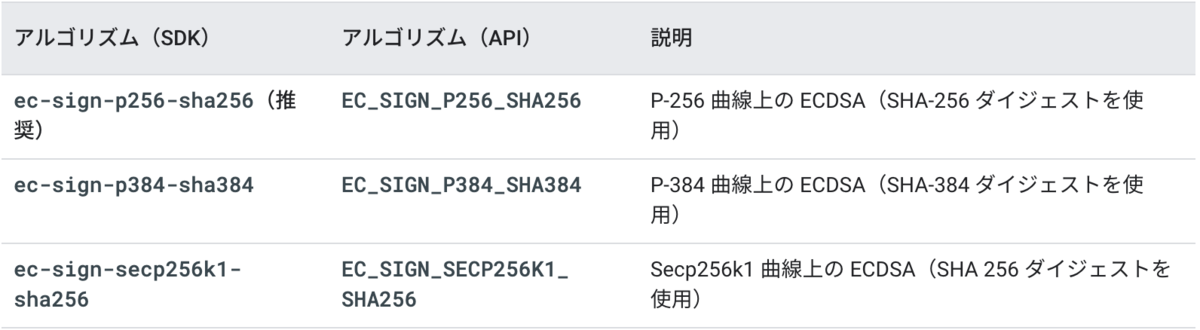
まず最初にSignDigestという関数が署名全体の処理を行う関数になっています。引数には、署名者のアドレスとSHA256ハッシュ化させてメッセージを入れます。

このハッシュ化されたメッセージをAsymmetricSignRequestというオブジェクトを作成して、AsymmetricSignという関数を呼び、KMSによる署名を作成します。返ってきた値はASN.1の構造をしているのでrecoverRS関数を呼び、 r, s をリカバリします。

func (k *KMSSigner) SignDigest(ctx context.Context, address common.Address, digest []byte) ([]byte, error) {
  // KMSで署名を行うためのデータ
    req := &kmspb.AsymmetricSignRequest{
        Name: keyVersion,
        Digest: &kmspb.Digest{
            Digest: &kmspb.Digest_Sha256{
                Sha256: digest,
            },
        },
    }

    // KMSに保存されてる秘密鍵を用いて署名が作成される
    // この作成された署名は公開鍵を用いて検証することができる
    result, err := k.client.AsymmetricSign(ctx, req)
    if err != nil {
        return nil, err
    }

    // ASN.1データ構造のsignatureからrとsをリカバリする
    r, s, err := recoverRS(result.Signature)
    if err != nil {
        return nil, err
    }
 
    // 後半の処理
    ...
}

recoverRSの関数の中はこのようになっています。goの標準パッケージとしてasn1が提供されているので、単純にそのパッケージ内にあるUnmarshalを呼び出します。

// recover R and S from KMS signature
func recoverRS(signature []byte) (r *big.Int, s *big.Int, err error) {
    sig := new(struct {
        R *big.Int
        S *big.Int
    })

    _, err = asn1.Unmarshal(out.Signature, sig)
    if err != nil {
        return nil, err
    }

    // 処理
    ...

    return sig.R, sig.S, nil
}

4-2-2. sの反転について

急に sの反転についてとありますが、この話は、前述した sの取りうる範囲についてです。ECDSA署名が有効であるには、3つの条件がありました。そのひとつ sは

0 < s < \text{secp256k1n/2 +1}

とすることが条件になります。EthereumのECDSA署名において、もし sが \text{secp256k1n}の半分よりも大きい場合は s' = \text{secp256k1n} - s（この演算を「 sの反転」と呼ぶことにする）を計算し、この値を使ってECDSA署名を作る必要があります。

var (
    secp256k1N, _  = new(big.Int).SetString("fffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141", 16)
    secp256k1halfN = new(big.Int).Div(secp256k1N, big.NewInt(2))
)

func recoverRS(signature []byte) (r *big.Int, s *big.Int, err error) {
    // 処理
    ...

    if sig.S.Cmp(secp256k1halfN) > 0 {
        sig.S = new(big.Int).Sub(secp256k1N, sig.S)
    }

    return sig.R, sig.S, nil
}

なぜ sは 0 \lt s \lt \text{secp256k1n}ではダメなのでしょうか？これはEIP-2の中でこの問題が指摘されています。

github.com

EIP-2で言われている問題をそのまま翻訳すると

0 < s < secp256k1Nの範囲での任意のs値を持つトランザクションを許可すると、トランザクションの不正性が 懸念される。なぜなら、s値をsからsecp256k1N - sに反転し、v値を（27 → 28, 28 → 27）を反転させても結 果として得られる署名は有効である。

つまり、 sを反転して得られた s'から (r, s', v')を作成しても、異なる署名結果であるのに有効と判断されてしまうということになります。これについて実際に値を変化させて検証します。（ v値については後述します）

前述の内容から sは以下のように求めることができました。

\tag{1} 　s \equiv {(h(m) + ar) \over k} \bmod l

「 sの反転」とは (1)の sに対して、

s' = l -s

として s'とおきます。この s'から u'を求めると

\begin{aligned} u' &\equiv s'^{-1}h(m) \bmod l \\ &\equiv {1 \over l -s} h(m) \bmod l \\ &\equiv s^{-1} {s \over l- s} h(m) \bmod l \\ &\equiv s^{-1} {s \over l- s} h(m) \bmod l - l (s^{-1}{1 \over l-s}h(m)) \bmod l \\ &\equiv s^{-1}{{s-l} \over l-s }h(m) \bmod l \\ &\equiv s^{-1} \lbrace -1 \times ({l-s \over l-s}) \rbrace h(m) \bmod l \\ &\equiv -s^{-1}h(m) \bmod l \end{aligned}

となり、 u'と uの関係は以下のようになります。

u' = -u

vについても同様で、 v'= -vとなり、 u', v'から

\begin{aligned} u'P +v'A &= -uP +-vA \\ &= -(uP+ vA) \\ &= -kP \end{aligned}

点PとQのx座標の値は同じ

となるので、楕円曲線上の点のマイナスは y座標の正負をさせるだけで x座標の値は変わりません。

つまり、 (*)は両辺の x座標の点が同じかどうかを検証しているので、反転させた s'で評価をしても同じ検証結果が得られます。

そのためEIP-2では sの範囲を 0 \lt s \lt \text{secp256k1n}/2 +1に制限し、もしこの範囲外に sがある場合は、その署名を無効することでこのような問題を防いでいます。

4-2-3. v値について

r, sをリカバリできたら最後に v値の計算です。 v値は rを x座標の値とする曲線上の点を一意に定めるための値でした。 v \in { 0, 1}の範囲で (r, s, v)の有効性を検証し、有効性が示された時の v値がECDSA署名に含まれます。

今では v値が 0, 1の場合は古いバージョンとして存在していて、それに 27を足した 27, 28が v値として署名に含まれます。また v値についてメインネットやテストネットなどのネットワークを区別するために、chainIDを含めた v値がEIP-155で提案されています。今回はこの説明はしませんが、詳しく知りたい人はこちらをご覧ください。

vは 0か 1のどちらかで正しい署名が作成できるので、2回検証を回して、それによってリカバリされるアドレスと署名者のアドレスを比較して同じ場合に、その値を v値にして最後に27を足して、署名の完成とします。

func (k *KMSSigner) SignDigest(ctx context.Context, address common.Address, digest []byte) ([]byte, error) {
    // 処理
    ...

    sig := make([]byte, 65)
    // r値
    copy(sig[:32], r.Bytes())
    // s値
    copy(sig[32:64], s.Bytes())
 
    for _, v := range []int{0, 1} {
        sigv := append(sig, byte(v))
        publicKey, err := secp256k1.RecoverPubkey(digest, sigv)

        if err != nil {
            return nil, err
        }

        verified := crypto.VerifySignature(publicKey, digest, sig[:len(sig)-1])
        addrA := common.BytesToAddress(crypto.Keccak256(publicKey[1:])[12:])

        if (verified && reflect.DeepEqual(addrA.Bytes(), address.Bytes())) {
            sig = append(sig, byte(v))
            break
        }
    }

    sig[64] += 27

    return sig, nil
}

以上、EthereumにおけるECDSA署名の作成方法について実際のコードを交えながら見ていきました。最後に、この得られた署名から公開鍵をどのようにリカバリするかを考えます。

4-2-4. ECDSA署名から公開鍵のリカバリ

署名の検証に関してはコントラクト上で行われます。ECDSA.recover によってアドレスが得られるので、得られたアドレスと署名者のアドレスを比較します。（この関数ではECDSA署名から公開鍵が得られ、内部でEthereumのアドレス形式に変換されています。）

address recoverdAddress = ECDSA.recover(digest, voucher.signature);
require(signerAddress == recoverdAddress, "address does not match");

実際にどのように公開鍵がリカバリされているのか見ていきます。

rと vから署名の際に選んだ公開鍵が一意に特定でき、それを Rとおく。

R= (r, y) = (u_1 + u_2a)P

Rと署名とハッシュ化された平文 mに対して以下のように計算すると、

\begin{aligned} Q &= r^{-1}(sR- h(m)P) \\ & = r^{-1}\lbrace s(u_1+u_2a)P - h(m)P \rbrace \\ &=r^{-1}\lbrace skP - h(m)P \rbrace \\ &= r^{-1} \lbrace {(h(m)+ ar) \over k } \times k P - h(m)P \rbrace \\ &= r^{-1}arP \\ &= aP \end{aligned}

となり、公開鍵が導出されます。つまり、署名が正しければ導出された公開鍵と署名に使用した公開鍵が一致することがわかります。

実際 Rの x座標の rが満たすべき条件というのがあり、このSEC 1: Elliptic Curve Cryptographyで説明されています。詳しくはそちらをご覧ください。

以上より、ECDSA署名の作成と検証することができました。

5. さいごに

今回は、楕円曲線暗号の概要とCloud KMSを用いたECDSA署名の作成・検証方法をコードと一緒に見てきました。

冒頭にも書きましたが、大学で代数学を勉強した程度なので理解が間違っている部分等あるかもしれません。なので、もしそのような箇所があればぜひご指摘いただけると嬉しいです。

Gaudiyでは、このようにブロックチェーンが絡んだ実装もあれば、普通のWebアプリケーション開発の実装もあります。個人的には好きな分野なので、興味ある方いたらぜひお話ししたいです！

meety.net